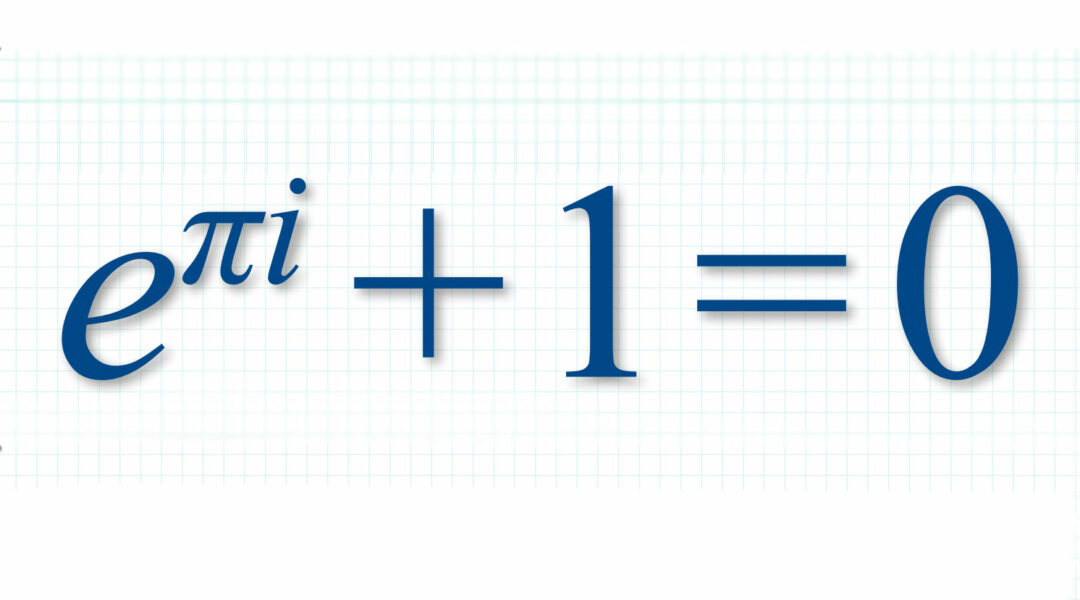
Världens vackraste ekvation
De imaginära talen, fysiken och frågan som blir oundviklig: Upptäcker vi människor matematiken, eller uppfinner vi den?
Året var 1982, det var sommar och VM i fotboll hölls i Spanien. Några av VM-historiens största drabbningar ägde rum: Italien mot Brasilien slutade 3–2 till Paolo Rossi. Frankrike mot Tyskland i semifinalen, Frankrike förlorade på straffar efter en galen förlängning. Smärta och sorg. Glädje och tårar. Vi minns profilerna, Sokrates, Falcao, Rossi och även Maradona visade upp sig på världsscenen men hans första VM slutade i frustration, utvisning och förnedring. Målvakten Schumachers tackling mot Battiston borde resulterat i en dom för överfall, men gav inte ens en varning. Zicos frisparkar var nästan overkliga, som om de kom från en annan värld.
Jag minns vilken fascination det väckte i mig. Det här är matematik – något större än att bara räkna med plus, minus och multiplikation.
Min bror Michael och jag spelade fotboll dagarna i ända. En vecka tillbringade vi med mormor och hennes sedan något år nya man i en sommarstuga i Hedekas, en bit norr om Uddevalla. En kväll började vi tala matematik. Jo, du vet ju att roten ur 9 är 3 (eftersom 3 x 3 = 9), sa mormors man och fortsatte, men vet du vad roten ur minus 1 är?
Frågan är inte enkel. Det kan inte vara minus ett eftersom två negativa tal som multipliceras med varandra ger ett positivt tal, till exempel (-1) x (-1) = 1. Det går således inte att hitta ett »vanligt« tal som är lika med roten ur minus ett. Testa på en miniräknare, i er smartphone eller i excel så får ni se. Man får då ett »error/fel« svar. Roten ur negativa tal har man genom historien skytt som barn skyr elden, åtminstone fram till 1500-talet. Då började man nämligen räkna med detta märkliga tal, som ett hjälpmedel för att hitta lösningar till vissa ekvationer.
Jag minns, där i Hedekas, hur min mormors nya man, Gunnar, skrev ner ett i, och sa, svaret är i. Och så tillade han att i står för imaginär, det är ett imaginärt tal. Tar man i gånger sig själv så blir svaret -1. Roten ur -1 är alltså i:
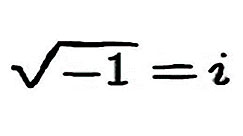
Jag minns vilken fascination det väckte i mig. Det här är matematik – något större än att bara räkna med plus, minus och multiplikation.
Det är värt att göra några reflektioner. Operationen roten ur har en geometrisk tolkning. Har man en kvadrat med arean 9 kvadratmeter så ger roten ur den här arean längden på sidan i kvadraten, alltså 3 meter. Men inga kvadrater kan ha en negativ area, alltså saknar roten ur ett negativt tal en uppenbar geometrisk mening. Man kan då ställa frågan om det imaginära talet i finns i verkligheten eller om det bara är en matematisk konstruktion.
Det intressanta är nu att även ett så märkligt tal som i långt senare kom att få en omfattande tillämpning i fysiken.
Det här väcker också den större frågan om matematikens natur. Upptäcker vi människor matematiken eller uppfinner vi den? Finns i i verkligheten eller är det något vi skapat? Talet i har också väckt förundran bland tänkare genom historien. Det var René Descartes (1596–1650) som gav talet sitt namn, i för imaginär. Gottfried Wilhelm von Leibniz (1646–1716) skrev i början av 1700-talet att »imaginära tal är en fin och vacker tillflykt för den gudomliga anden, nästan som en amfibie mellan varat och icke-varat«.
Det intressanta är nu att även ett så märkligt tal som i långt senare kom att få en omfattande tillämpning i fysiken. Det används hela tiden när man räknar på elektriska kretsar och det spelar en central roll i kvantfysiken. I Schrödinger-ekvationen, kvantfysikens centrala ekvation, ingår i explicit.
Schrödingerekvationen är en vågekvation, där partiklar, exempelvis elektroner, beskrivs som en våg, och de resultat man får när man räknar med den är oerhört exakta. Jag tror inte att någon vetenskaplig teori har testats så väl som kvantfysiken, och den står sig – än så länge – alldeles utmärkt.
Men i den har man alltså ett imaginärt tal, ett tal som man skulle kunna säga att vi människor skapat. Det här väckte förundran men även visst motstånd bland kvantmekanikens fäder.
Det faktum att abstrakta matematiska konstruktioner, som till en början inte verkar ha något alls med vår fysiska omvärld att göra, senare får stor betydelse inom fysiken begränsar sig inte bara till det imaginära talet i.
Till en början tänkte man att dessa så kallade icke-euklidiska rum inte hade något med vår fysiska verklighet att göra. Men sedan kom Albert Einstein med sin allmänna relativitetsteori.
Vi har även den så kallade icke-euklidiska geometrin. Bernhard Riemann (1826–1866), en av de riktigt tunga matematikerna på 1800-talet, var en av dem som funderade över grundläggande antaganden inom geometrin. Föreställ er en punkt bredvid en oändligt lång linje (på ett obegränsat stort plant papper). Fråga er sedan hur många linjer man kan dra igenom denna punkt, som inte någonstans skär den första linjen. Svaret är bara en – den som går helt parallellt med den första linjen. Detta var ett grundläggande axiom hos Euklides.

Men Riemann tänkte fritt. Vad händer frågade han sig, om detta antagande inte gäller, vad får det för konsekvenser för geometrin? På så sätt kunde man bygga upp helt andra geometriska rum än de vi upplever omkring oss.
Till en början tänkte man att dessa så kallade icke-euklidiska rum inte hade något med vår fysiska verklighet att göra. Men sedan kom Albert Einstein med sin allmänna relativitetsteori, den som beskriver hur gravitationen kröker vår rum-tid. I denna värld är rummet och tiden sammanbundna på ett fascinerande sätt. Har vi till exempel ett tungt objekt så kröks rummet runt det. Ja, inte bara rummet utan också tiden, man talar om att själva rumtiden är krökt. Rummet och tiden går inte riktigt att separera. Tiden utanför ett tungt astronomiskt objekt går lite långsammare, och precis utanför ett svart hål tickar tiden inte på alls.
Runt en stor stjärna kröks rummet så vi kan se en stjärna som ligger bakom den stora stjärnan (som egentligen borde täcka den). Stjärnan där bakom syns då som en ring runt den första. Ljuset har böjts av. Det här fenomenet kallas för Einstein-ring. Jag rekommenderar läsaren att googla »Einstein ring« och njuta av bilder på ett spännande astronomiskt fenomen.

När Einstein utvecklade sin allmänna relativitetsteori förlitade han sig på den icke-euklidiska geometrin. Återigen ett exempel på hur abstrakta matematiska konstruktioner visade sig ha stor betydelse inom fysiken.
Hela den här frågan om varför matematiken – en abstrakt mänsklig konstruktion – kommit att bli så otroligt användbar när det gäller att beskriva världen är intressant. År 1960 skrev exempelvis kvantfysikern Eugene Wigner en artikel kallad The Unreasonable Effectiveness of Mathematics in the Natural Sciences där han går på djupet med frågan.
Kanske är det helt enkelt evolutionärt: man utvecklar en massa olika matematik, till en början i det abstrakta, men sedan får den matematik som visar sig mest användbar också störst spridning. Den fysiska verkligheten blir ett slags såll som sorterar bort den mest världsfrånvända matematiken och ökar intresset för det som är användbart.
Låt oss återvända till det imaginära talet i. Det ingår nämligen i en ekvation som kallas för Eulers identitet, efter Leonhard Euler (1707–1783), född i Basel men huvudsakligen verksam i Sankt Petersburg.
Låt mig först påminna om vad upphöjt till betyder. Tar man exempelvis 2 upphöjt till 5, alltså 25 så betyder det två gånger sig självt fem gånger, alltså 25 = 2 x 2 x 2 x 2 x 2. Men beakta nu frågan: vad innebär det att ta ett tal 2 upphöjt till i? Hur multiplicerar man 2 med sig självt ett imaginärt antal gånger? Det går ju knappt att föreställa sig.
Men Euler finner en lösning på problemet och i ett specialfall får han följande resultat, som kallas Eulers identitet:
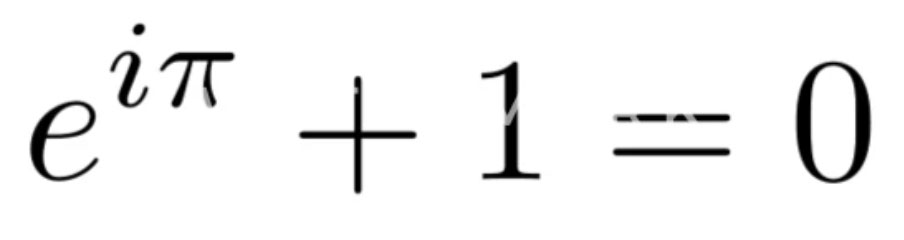
Här ingår e, ett tal som är ungefär 2,718 … (decimalutvecklingen fortsätter i all oändlighet). Talet e har en särställning i matematik och fysik. Det används i samband med beräkningar av förlopp med exponentiell tillväxt och har nämligen den alldeles speciella egenskapen att lutningen på funktionen e upphöjt till x, är lika med funktionen själv (matematiker säger att derivatan av ex är ex).
I ekvationen ingår även π, som är en annan av matematikens älsklingar, och beskriver relationen mellan en cirkels omkrets och dess diameter. Både π och e är irrationella tal med oändligt långa decimalutvecklingar.
Eulers identitet visar nu alltså att om man tar talet e och upphöjer det till π multiplicerat med i så får man – enligt den matematiska konstens alla regler – minus 1. Alla konstiga, mystiska oändliga decimalutvecklingar hos e och π har bara försvunnit, trollats bort.
Matematiska skönheter
Detta är tredje delen i artikelserien Matematikens skönheter. Läs första delen här.
Ytterligare en variant på det här som jag är närmast omåttligt förtjust i är att ii är lika med e-π/2. Om man tar det imaginära talet i och multiplicerar det med sig självt ett imaginärt antal gånger, så trillar plötsligt e-π/2 (cirka 0,2079 …) ut. Det är fascinerande med dessa oväntade genvägar mellan den reella och den imaginära världen.
Jag undrar vad pythagoréerna skulle ha tänkt om detta. Bland matematiker ses Eulers identitet ofta som världens vackraste ekvation.
***
Läs även: Matematik på liv och död
Året var 1982, det var sommar och VM i fotboll hölls i Spanien. Några av VM-historiens största drabbningar ägde rum: Italien mot Brasilien slutade 3–2 till Paolo Rossi. Frankrike mot Tyskland i semifinalen, Frankrike förlorade på straffar efter en galen förlängning. Smärta och sorg. Glädje och tårar. Vi minns profilerna, Sokrates, Falcao, Rossi och även Maradona visade upp sig på världsscenen men hans första VM slutade i frustration, utvisning och förnedring. Målvakten Schumachers tackling mot Battiston borde resulterat i en dom för överfall, men gav inte ens en varning. Zicos frisparkar var nästan overkliga, som om de kom från en annan värld.
Jag minns vilken fascination det väckte i mig. Det här är matematik – något större än att bara räkna med plus, minus och multiplikation.
Min bror Michael och jag spelade fotboll dagarna i ända. En vecka tillbringade vi med mormor och hennes sedan något år nya man i en sommarstuga i Hedekas, en bit norr om Uddevalla. En kväll började vi tala matematik. Jo, du vet ju att roten ur 9 är 3 (eftersom 3 x 3 = 9), sa mormors man och fortsatte, men vet du vad roten ur minus 1 är?
Frågan är inte enkel. Det kan inte vara minus ett eftersom två negativa tal som multipliceras med varandra ger ett positivt tal, till exempel (-1) x (-1) = 1. Det går således inte att hitta ett »vanligt« tal som är lika med roten ur minus ett. Testa på en miniräknare, i er smartphone eller i excel så får ni se. Man får då ett »error/fel« svar. Roten ur negativa tal har man genom historien skytt som barn skyr elden, åtminstone fram till 1500-talet. Då började man nämligen räkna med detta märkliga tal, som ett hjälpmedel för att hitta lösningar till vissa ekvationer.
Jag minns, där i Hedekas, hur min mormors nya man, Gunnar, skrev ner ett i, och sa, svaret är i. Och så tillade han att i står för imaginär, det är ett imaginärt tal. Tar man i gånger sig själv så blir svaret -1. Roten ur -1 är alltså i:
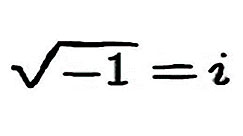
Jag minns vilken fascination det väckte i mig. Det här är matematik – något större än att bara räkna med plus, minus och multiplikation.
Det är värt att göra några reflektioner. Operationen roten ur har en geometrisk tolkning. Har man en kvadrat med arean 9 kvadratmeter så ger roten ur den här arean längden på sidan i kvadraten, alltså 3 meter. Men inga kvadrater kan ha en negativ area, alltså saknar roten ur ett negativt tal en uppenbar geometrisk mening. Man kan då ställa frågan om det imaginära talet i finns i verkligheten eller om det bara är en matematisk konstruktion.
Det intressanta är nu att även ett så märkligt tal som i långt senare kom att få en omfattande tillämpning i fysiken.
Det här väcker också den större frågan om matematikens natur. Upptäcker vi människor matematiken eller uppfinner vi den? Finns i i verkligheten eller är det något vi skapat? Talet i har också väckt förundran bland tänkare genom historien. Det var René Descartes (1596–1650) som gav talet sitt namn, i för imaginär. Gottfried Wilhelm von Leibniz (1646–1716) skrev i början av 1700-talet att »imaginära tal är en fin och vacker tillflykt för den gudomliga anden, nästan som en amfibie mellan varat och icke-varat«.
Det intressanta är nu att även ett så märkligt tal som i långt senare kom att få en omfattande tillämpning i fysiken. Det används hela tiden när man räknar på elektriska kretsar och det spelar en central roll i kvantfysiken. I Schrödinger-ekvationen, kvantfysikens centrala ekvation, ingår i explicit.
Schrödingerekvationen är en vågekvation, där partiklar, exempelvis elektroner, beskrivs som en våg, och de resultat man får när man räknar med den är oerhört exakta. Jag tror inte att någon vetenskaplig teori har testats så väl som kvantfysiken, och den står sig – än så länge – alldeles utmärkt.
Men i den har man alltså ett imaginärt tal, ett tal som man skulle kunna säga att vi människor skapat. Det här väckte förundran men även visst motstånd bland kvantmekanikens fäder.
Det faktum att abstrakta matematiska konstruktioner, som till en början inte verkar ha något alls med vår fysiska omvärld att göra, senare får stor betydelse inom fysiken begränsar sig inte bara till det imaginära talet i.
Till en början tänkte man att dessa så kallade icke-euklidiska rum inte hade något med vår fysiska verklighet att göra. Men sedan kom Albert Einstein med sin allmänna relativitetsteori.
Vi har även den så kallade icke-euklidiska geometrin. Bernhard Riemann (1826–1866), en av de riktigt tunga matematikerna på 1800-talet, var en av dem som funderade över grundläggande antaganden inom geometrin. Föreställ er en punkt bredvid en oändligt lång linje (på ett obegränsat stort plant papper). Fråga er sedan hur många linjer man kan dra igenom denna punkt, som inte någonstans skär den första linjen. Svaret är bara en – den som går helt parallellt med den första linjen. Detta var ett grundläggande axiom hos Euklides.

Men Riemann tänkte fritt. Vad händer frågade han sig, om detta antagande inte gäller, vad får det för konsekvenser för geometrin? På så sätt kunde man bygga upp helt andra geometriska rum än de vi upplever omkring oss.
Till en början tänkte man att dessa så kallade icke-euklidiska rum inte hade något med vår fysiska verklighet att göra. Men sedan kom Albert Einstein med sin allmänna relativitetsteori, den som beskriver hur gravitationen kröker vår rum-tid. I denna värld är rummet och tiden sammanbundna på ett fascinerande sätt. Har vi till exempel ett tungt objekt så kröks rummet runt det. Ja, inte bara rummet utan också tiden, man talar om att själva rumtiden är krökt. Rummet och tiden går inte riktigt att separera. Tiden utanför ett tungt astronomiskt objekt går lite långsammare, och precis utanför ett svart hål tickar tiden inte på alls.
Runt en stor stjärna kröks rummet så vi kan se en stjärna som ligger bakom den stora stjärnan (som egentligen borde täcka den). Stjärnan där bakom syns då som en ring runt den första. Ljuset har böjts av. Det här fenomenet kallas för Einstein-ring. Jag rekommenderar läsaren att googla »Einstein ring« och njuta av bilder på ett spännande astronomiskt fenomen.

När Einstein utvecklade sin allmänna relativitetsteori förlitade han sig på den icke-euklidiska geometrin. Återigen ett exempel på hur abstrakta matematiska konstruktioner visade sig ha stor betydelse inom fysiken.
Hela den här frågan om varför matematiken – en abstrakt mänsklig konstruktion – kommit att bli så otroligt användbar när det gäller att beskriva världen är intressant. År 1960 skrev exempelvis kvantfysikern Eugene Wigner en artikel kallad The Unreasonable Effectiveness of Mathematics in the Natural Sciences där han går på djupet med frågan.
Kanske är det helt enkelt evolutionärt: man utvecklar en massa olika matematik, till en början i det abstrakta, men sedan får den matematik som visar sig mest användbar också störst spridning. Den fysiska verkligheten blir ett slags såll som sorterar bort den mest världsfrånvända matematiken och ökar intresset för det som är användbart.
Låt oss återvända till det imaginära talet i. Det ingår nämligen i en ekvation som kallas för Eulers identitet, efter Leonhard Euler (1707–1783), född i Basel men huvudsakligen verksam i Sankt Petersburg.
Låt mig först påminna om vad upphöjt till betyder. Tar man exempelvis 2 upphöjt till 5, alltså 25 så betyder det två gånger sig självt fem gånger, alltså 25 = 2 x 2 x 2 x 2 x 2. Men beakta nu frågan: vad innebär det att ta ett tal 2 upphöjt till i? Hur multiplicerar man 2 med sig självt ett imaginärt antal gånger? Det går ju knappt att föreställa sig.
Men Euler finner en lösning på problemet och i ett specialfall får han följande resultat, som kallas Eulers identitet:
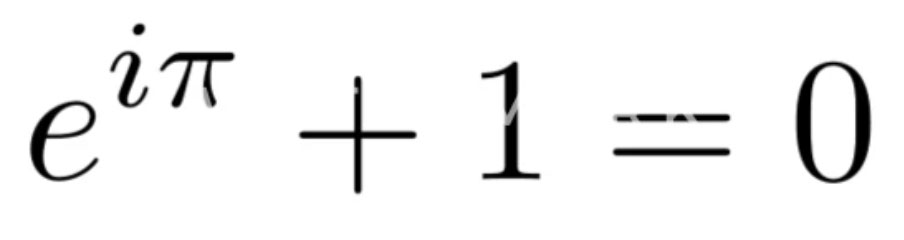
Här ingår e, ett tal som är ungefär 2,718 … (decimalutvecklingen fortsätter i all oändlighet). Talet e har en särställning i matematik och fysik. Det används i samband med beräkningar av förlopp med exponentiell tillväxt och har nämligen den alldeles speciella egenskapen att lutningen på funktionen e upphöjt till x, är lika med funktionen själv (matematiker säger att derivatan av ex är ex).
I ekvationen ingår även π, som är en annan av matematikens älsklingar, och beskriver relationen mellan en cirkels omkrets och dess diameter. Både π och e är irrationella tal med oändligt långa decimalutvecklingar.
Eulers identitet visar nu alltså att om man tar talet e och upphöjer det till π multiplicerat med i så får man – enligt den matematiska konstens alla regler – minus 1. Alla konstiga, mystiska oändliga decimalutvecklingar hos e och π har bara försvunnit, trollats bort.
Matematiska skönheter
Detta är tredje delen i artikelserien Matematikens skönheter. Läs första delen här.
Ytterligare en variant på det här som jag är närmast omåttligt förtjust i är att ii är lika med e-π/2. Om man tar det imaginära talet i och multiplicerar det med sig självt ett imaginärt antal gånger, så trillar plötsligt e-π/2 (cirka 0,2079 …) ut. Det är fascinerande med dessa oväntade genvägar mellan den reella och den imaginära världen.
Jag undrar vad pythagoréerna skulle ha tänkt om detta. Bland matematiker ses Eulers identitet ofta som världens vackraste ekvation.
***
Läs även: Matematik på liv och död